2014年陕西中考数学命题方向、冲刺攻略

西安查字典中考网讯：2014年陕西中考数学试题基本上会按照去年的特点，力争稳中有变，变中求新，今年的考点不变，空间图形、角、平行线的判定与性质，方程与不等式的解法，等腰三角形和直角三角形的判定和性质，全等三角形与判定三角形的性质，平行四边形的性质，圆的性质，图形的平移、对称、旋转，还有概率与统计题，一次方程、一次函数与方程不等式的运用题，是21题或者22题，二次函数与几何的综合题比如是24题，最后的压轴题是实践与综合的探究题，就是第25题，针对以上考点，同学们要重点复习掌握四基，就是基础知识、基本技能和基本的思想方法，训练思维，提升自己的能力，积累解题的基本经验。现在离中考只有一个月了，冲刺复习的时候，考生应该注意什么?有哪些重点要特别注意呢?

1.重视基础和细节，合理例练精勿滥；中考复习特别是考前一个月的复习，既要强调主干内容，又不能忽视细节．具体操作上，就是要求每一位考生，在训练时把运算进行到底，把推理进行到底，不因显然而跳过任何一个环节，不因事小而不为．

2.梳理知识建网络，四大领域在心间；遗漏的知识要补充；模糊的概念要明晰；零散的内容要整合；初浅的理解要深化。要会转化知识联系；要会探究两知一拢（由已知想可知，由未知想须知）；要会阅读审题深究

3.综合运用提能力，专题复习见成效；在前期复习的基础上，通过练习、测验、模拟考试，都会发现自己很多失分点，从错题中总结归纳自己的知识漏洞，这是最好的方式。在冲刺阶段主要是两个方面，除了上面说的之外，还有一个就是专题训练和模拟强化，专题训练就是经过在第一轮复习的接触上，专题训练要突出重点，第一个阶段复习的弱点，第二个就是课标教材中的重点，方程、函数、不等式、三角形、四边形、圆、概率与统计，第三个是中考试题中的热点问题，比如说运动题、操作题、开放题啊，还有图表信息题，专题训练的方法就是讲练结合，练是基础，评是精华，在老师讲评的时候非常重要，在讲评前必须自己独立思考，完成练习。

4.因人而异，针对复习。考生对知识、方法掌握的程度不同，在最后阶段冲刺复习的方法也不同，程度好一点的考生，对基础知识和方法都掌握得比较好，这时候最后阶段的复习，重点应该放在对细节问题的复习上，往往对简单基础的知识比较忽视，在中考中会出现比较简单、细节不够注意的错误，这些孩子要把细节问题，特别是平时出现的细节错误要加强复习。有一些考生在非常熟悉的题目上，他没有认真审题，可能某些词语变化了，对题目造成很大理解上的偏差，导致错误。再一个程度好一点的考生，在压轴题上，难度较大的题上要多下一些工夫，经过长期复习，对压轴题的认识可能是散在的，针对自己掌握的程度和老师的指导，把压轴题的类型分类，归纳一类题的解题方法和思路，涉及的方式和考点是你曾经训练的，可以把这些思路用在考试中。

心态决定成败。中考，不仅是能力的比拼，也是心理的较量，任何时候都不要忘记：中考复习的主体是考生自己，比关注命题信息更为重要的是关注自己的状态；能力是基础，心态是保障。

熟知试卷考题对应考点，掌握应试技巧。

如图，点C是⊙O弦AB上的一动点，点D为⊙O上一动点，连接OC、CD，且始终有DCO=90?，若AB=,则CD的最大值为

．

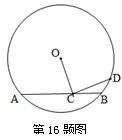
第17题：主要考查学生对代数式中多项式与分式的恒等变形（化简求值）能力（难度0.70）

第20题：主要考查学生灵活运用锐角三角函数的概念来解决现实生活中，用Rt△建模的实际问题，并通过解Rt△，而使问题得以解决的能力；（高度、宽度、深度；某一个几何图形的参数或面积等）（难度0.65）

第24题：主要考查学生进一步对二次函数的认识及二次函数与直线、三角形、四边形间的相依关系，同时综合考查学生运用一元二次方程、三角函数，两个三角形全等、相似及轴对称、中心对称、平移等知识处理和解决问题的能力。（难度0.50）

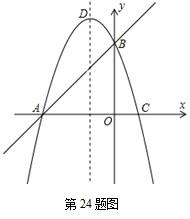
如图，抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．（1）求抛物线的解析式；

（2）点P从点D出发，沿对称轴向下以每秒1个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，以P、B、C为顶点的三角形是直角三角形？

第25题：主要通过组合的几何图形作为载体，综合考查学生运用所学的知识进行数学抽象、数学推理、数学建模的能力。通常是以三角形、特殊四边形、圆为基本图形，进行组合构成现实世界中存在或可能存在的事实进行探索研究。（设想：①使学生能够充分运用几何演绎进行推理，代数演绎进行科学合理运算，解析演绎进行数学建模；②图形简单、美观、图形的元素间关系清晰、建模有难度；③以探究式设问（总体以题问题或探究）难度与去年持平。（难度0.40）本试题起点低、落点高，前边两个问题简单，后面一个问题较难，因此在解决25题最后一问时一定要会应用前边两问题的结论或解法。

考生在熟知试卷考题对应考点的同时训练答卷的时间分配，通常情况选择题、填空题用时为2530分钟，第17题第23题时间控制在50分钟内，第24题用时15分钟，第25题用时20分钟，最后留5分钟通览全卷。小题一定要一次到位，涂到卡上，填到空上，解答题要写详细的过程，而且要详略得当，字迹要工整，难题不能放弃，会几步就写几步，该得分的拿到手以后就不留遗憾。

熟知试卷考题对应考点，掌握应试技巧。

如图，点C是⊙O弦AB上的一动点，点D为⊙O上一动点，连接OC、CD，且始终有DCO=90?，若AB=,则CD的最大值为

．

第17题：主要考查学生对代数式中多项式与分式的恒等变形（化简求值）能力（难度0.70）

第20题：主要考查学生灵活运用锐角三角函数的概念来解决现实生活中，用Rt△建模的实际问题，并通过解Rt△，而使问题得以解决的能力；（高度、宽度、深度；某一个几何图形的参数或面积等）（难度0.65）

第24题：主要考查学生进一步对二次函数的认识及二次函数与直线、三角形、四边形间的相依关系，同时综合考查学生运用一元二次方程、三角函数，两个三角形全等、相似及轴对称、中心对称、平移等知识处理和解决问题的能力。（难度0.50）

如图，抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．（1）求抛物线的解析式；

（2）点P从点D出发，沿对称轴向下以每秒1个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，以P、B、C为顶点的三角形是直角三角形？

第25题：主要通过组合的几何图形作为载体，综合考查学生运用所学的知识进行数学抽象、数学推理、数学建模的能力。通常是以三角形、特殊四边形、圆为基本图形，进行组合构成现实世界中存在或可能存在的事实进行探索研究。（设想：①使学生能够充分运用几何演绎进行推理，代数演绎进行科学合理运算，解析演绎进行数学建模；②图形简单、美观、图形的元素间关系清晰、建模有难度；③以探究式设问（总体以题问题或探究）难度与去年持平。（难度0.40）本试题起点低、落点高，前边两个问题简单，后面一个问题较难，因此在解决25题最后一问时一定要会应用前边两问题的结论或解法。

考生在熟知试卷考题对应考点的同时训练答卷的时间分配，通常情况选择题、填空题用时为2530分钟，第17题第23题时间控制在50分钟内，第24题用时15分钟，第25题用时20分钟，最后留5分钟通览全卷。小题一定要一次到位，涂到卡上，填到空上，解答题要写详细的过程，而且要详略得当，字迹要工整，难题不能放弃，会几步就写几步，该得分的拿到手以后就不留遗憾。