中考数学:一次函数知识点整合
发布时间:2016-11-16 09:32:11来源:查字典-中考网
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数。
特别地,当一次函数y=kx+b中的b为0时,y=kx(k为常数,k≠0)这时,y叫做x的正比例函数。
一、一次函数、正比例函数图像的主要特征:
所有一次函数的图像都是一条直线
一次函数y=kx+b的图像是经过点(0,b)的直线;正比例函数y=kx的图像是经过原点(0,0)的直线。
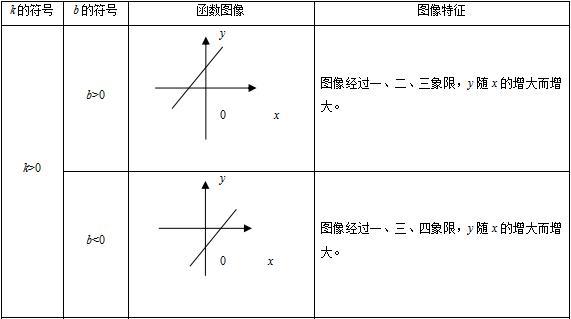
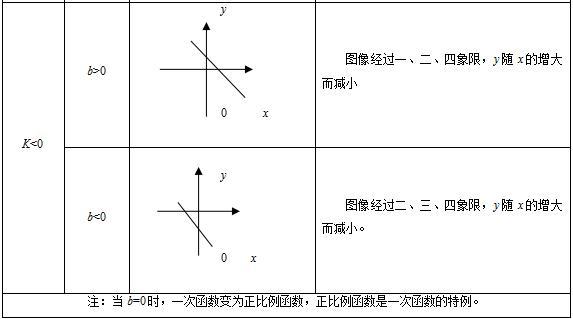
直线位置与k,b的关系:
1、k>0直线向上的方向与x轴的正方向所形成的夹角为锐角;
2、k<0直线向上的方向与x轴的正方向所形成的夹角为钝角;
3、b>0直线与y轴交点在x轴的上方;
4、b=0直线过原点;
5、b<0直线与y轴交点在x轴的下方;
二、正比例函数的性质
一般地,正比例函数y=kx有下列性质:
(1)当k>0时,图像经过第一、三象限,y随x的增大而增大;
(2)当k<0时,图像经过第二、四象限,y随x的增大而减小。
三、一次函数的性质
一般地,一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而增大
(2)当k<0时,y随x的增大而减小
四、正比例函数和一次函数解析式的确定
确定一个正比例函数,就是要确定正比例函数定义式y=kx(k≠0)中的常数k。确定一个一次函数,需要确定一次函数定义式y=kx+b(k≠0)中的常数k和b。解这类问题的一般方法是待定系数法。
典型例题1:



解题反思:
本题主要考查的是一次函数和相似三角形的性质和判定,用含字母t的式子表示点C的坐标是解题的关键.
典型例题2:
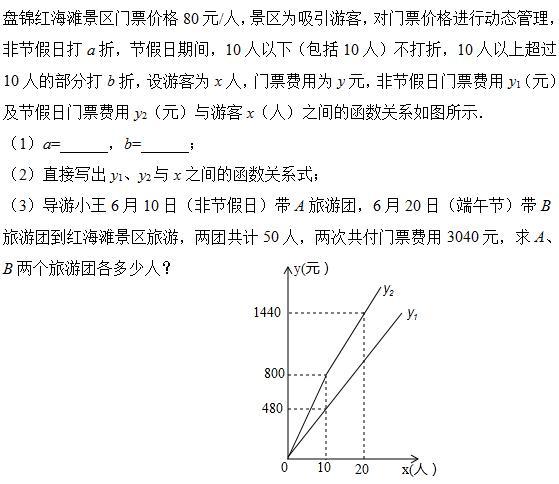


解题反思:
本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,准确识图获取必要的信息并理解打折的意义是解题的关键,要注意分情况讨论。