证明三角形对称的性质

根据等腰三角形的对称性还应有如下重要的性质，虽在证明中不能直接引用，但对于填空、选择则可直接运用，并且这些性质对今后的推理证明都有非常重要的作用。

①等腰三角形两腰上的中线相等

已知：在ABC 中，AB＝AC，若BD，CE分别是AC，AB边上的中线，则有BD＝CE。

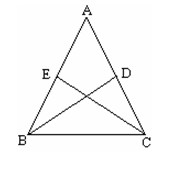
证明：∵BD，CE是AB，AC边上的中线(已知)

AD＝ AC，AE＝ AB(中线定义)

∵AB＝AC(已知)

AD＝AE

在ABD和ACE中，

ABD≌ACE(SAS)

BD＝CE(全等三角形对应边相等)。

②等腰三角形两腰上的高相等

已知：在ABC中，AB＝AC，如果BD，CE分别是AC，AB边上的高，那么BD＝CE。

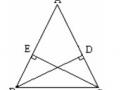
同学可以试着证明一下，还用全等三角形去证。

③等腰三角形两底角的平分线相等

已知：在ABC中，AB＝AC，如果BD，CE分别是ABC和ACB的平分线，那么BD＝CE。

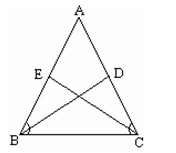
同学可利用全等三角形法证明。