初一初二数学提高系列资料汇总

重庆查字典中考网讯：小编给大家整理了初一初二数学提高系列资料，如有需要，请自行下载！

七年级上学期数学提高系列之一(有理数) 下载

点击查看

七年级上学期数学提高系列之二(整式的加减) 下载

点击查看

七年级上学期数学提高系列之三(一元一次方程) 下载

点击查看

七年级上学期数学提高系列之四(图形认识初步) 下载

点击查看

七年级上学期数学提高系列之衔接篇 下载

点击查看

点击查看

点击查看

点击查看

点击查看

点击查看

有理数

资料下载请点击！！

整数和分数的统称。正整数和正分数合称为正有理数，负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零3种数。由于任何一个整数或分数都可以化为十进循环小数，反之，每一个十进循环小数也能化为整数或分数，因此，有理数也可以定义为十进循环小数。有理数集是整数集的扩张。在有理数集内，加法、减法、乘法、除法（除数不为零）4种运算通行无阻。有理数的大小顺序的规定：如果a-b是正有理数，就称a大于b或b小于a，记作ab或b

整式的加减

资料下载请点击！！

整式的加减

同类项合并同类项去括号法

则添括号法则合并同类项法

则整式的加减法法则

同类项的识别

合并同类项的技巧

化简多项式的步骤

1.整式的加减

2.同类项合并同类项去括号法

3.添括号法则合并同类项法

4.整式的加减法法则

5.同类项的识别

6.合并同类项的技巧

7.化简多项式的步骤

一元一次方程

资料下载请点击！！

只含有一个未知数（即元），并且未知数的最高次数为1（即次）的整式方程叫做一元一次方程（英文名：linear equation with one unknown）。一元一次方程的标准形式（即所有一元一次方程经整理都能得到的形式）是ax+b=0（a，b为常数，x为未知数，且a0）。求根公式：x=-b/a。

方程特点

（1）该方程为整式方程。

（2）该方程有且只含有一个未知数。

（3）该方程中未知数的最高次数是1。

满足以上三点的方程，就是一元一次方程。

判断方法

要判断一个方程是否为一元一次方程，先看它是否为整式方程。若是，再对它进行整理。如果能整理为 ax+b=0（a0）的形式，则这个方程就为一元一次方程。里面要有等号，且分母里不含未知数。

变形公式

ax=-b（a，b为常数，x为未知数，且a0）

通常解法

去分母去括号移项合并同类项系数化为1。

两种类型

（1）总量等于各分量之和。将未知数放在等号左边，常数放在右边。如：x+2x+3x=6。

（2）等式两边都含未知数。如：300x+400=400x，40x+20=60x。

图形认识初步

资料下载请点击！！

一、 直线、相交线、平行线

1．线段、射线、直线三者的区别与联系 从图形、表示法、界限、端点个数、基本性质等方面加以分析。

2．线段的中点及表示

3．直线、线段的基本性质（用线段的基本性质论证三角形两边之和大于第三边）

4．两点间的距离（三个距离：点-点；点-线；线-线）

5．角（平角、周角、直角、锐角、钝角）

6．互为余角、互为补角及表示方法

7．角的平分线及其表示

8．垂线及基本性质（利用它证明直角三角形中斜边大于直角边）

9．对顶角及性质

10．平行线及判定与性质（互逆）（二者的区别与联系）

11．常用定理：①同平行于一条直线的两条直线平行（传递性）；②同垂直于一条直线的两条直线平行。

12．定义、命题、命题的组成

13．公理、定理

14．逆命题

二、三角形

1．定义（包括内、外角）

2．三角形的边角关系：

⑴角与角：

①内角和及推论；

②外角和；

③n边形内角和；

④n边形外角和。

⑵边与边：三角形两边之和大于第三边，两边之差小于第三边。

⑶角与边：在同一三角形中，

3．三角形的主要线段

讨论：①定义②线的交点三角形的心③性质 ① 高线②中线③角平分线④中垂线⑤中位线 ⑴一般三角形⑵特殊三角形：直角三角形、等腰三角形、等边三角形

4．特殊三角形（直角三角形、等腰三角形、等边三角形、等腰直角三角形）的判定与性质

5．全等三角形 ⑴一般三角形全等的判定（SAS、ASA、AAS、SSS） ⑵特殊三角形全等的判定：①一般方法②专用方法

6．三角形的面积 ⑴一般计算公式⑵性质：等底等高的三角形面积相等。

7．重要辅助线 ⑴中点配中点构成中位线；⑵加倍中线；⑶添加辅助平行线

8．证明方法

⑴直接证法：综合法、分析法

⑵间接证法反证法：①反设②归谬③结论 ⑶证线段相等、角相等常通过证三角形全等

⑷证线段倍分关系：加倍法、折半法 ⑸证线段和差关系：延结法、截余法 ⑹证面积关系：将面积表示出来

衔接篇

资料下载请点击！！

初中数学与小学数学的侧重点是不同的。小学数学侧重是打下数学的基础。因此，其内容主要是数、数与数之间的关系；各种量与计量的方法；各种基本运算、基本的数量关系；基本的图形认识及简单的周长、面积与体积计算；以及简单的代数知识等。 初中数学则侧重于培养学生的数学能力，包括计算能力、自学能力、分析问题与解决问题的能力、抽象逻辑思维的能力等。在内容上增加了复杂的平面几何知识，系统学习代数知识，运用方程解决实际问题；数扩展到有理数、实数；还有简单的一次函数与二次函数。

全等三角形

资料下载请点击！！

能够完全重合的两个三角形叫做全等三角形，而该两个三角形的三条边及三个角都对应相等。全等三角形是几何中全等的一种。是一个三角形通过平移，旋转或翻折后得到的新图形与这个图形全等。正常来说，验证两个全等三角形一般用边边边（SSS） 边角边（SAS) 角边角（ASA） 角角边（AAS) 和斜边，直角边（HL)来判定。 SSS同时否定AAA和ASS。

性质

1．全等三角形的对应角相等

2．全等三角形的对应边相等

3.能够完全重合的顶点叫对应顶点

4．全等三角形的对应边上的高对应相等。

5．全等三角形的对应角的角平分线相等。

6．全等三角形的对应边上的中线相等。

7．全等三角形面积和周长相等。

8．全等三角形的对应角的三角函数值相等。

判定过程

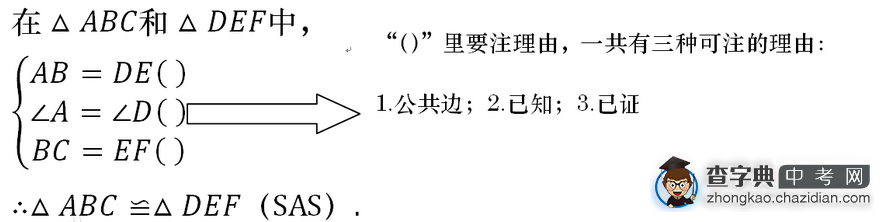
在第一行写要进行判定全等的两个三角形；

第二行画大括号，分别写判定的三个条件，并注明理由：

四种理由：

1.公共边；2.已知；3.已证；4.公共角；

最后一行，写两个三角形全等并注明理由.（如右图）(不严格要求写理由）

（若为直角三角形，在第二行须先写明两个直角相等并为90度，再写两个斜边、直角边分别相等）。

（例：RT△xxx与RT△xxx）

(提示：线段的垂直平分线上的一点到线段的两个端点的距离相等)

轴对称

资料下载请点击！！

如果沿某条在正中的直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴。对称轴绝对是一条直线。

如果一个函数图象关于一条直线x=a对称，那么它满足f(a-x)=f(a+x)；或f(x)=f(2a-x)。

圆是轴对称图形，直径所在的直线是圆的对称轴，圆有无数条对称轴。

实数

资料下载请点击！！

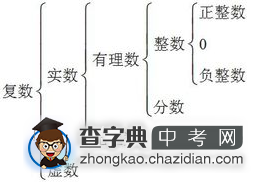
包括有理数和无理数。其中无理数就是无限不循环小数，有理数就包括整数和分数。数学上，实数直观地定义为和数轴上的点一一对应的数。本来实数仅称作数，后来引入了虚数概念，原本的数称作实数意义是实在的数。（任何实数都可在数轴上表示。）

实数可以分为有理数和无理数两类，或代数数和超越数两类，或正实数，负实数和零三类。实数集合通常用字母 R 表示。而R^n表示 n 维实数空间。实数是不可数的。实数是实数理论的核心研究对象。

实数可以用来测量连续的量。理论上，任何实数都可以用无限小数的方式表示，小数点的右边是一个无穷的数列（可以是循环的，也可以是非循环的）。在实际运用中，实数经常被近似成一个有限小数（保留小数点后 n 位，n为正整数，包括整数）。在计算机领域，由于计算机只能存储有限的小数位数，实数经常用浮点数来表示。

1）相反数（只有符号不同的两个数，它们的和为零，我们就说其中一个是另一个的相反数） 实数a的相反数是-a，a和-a在数轴上到原点0的距离相等。）

2）绝对值（在数轴上另一个数与a到原点0的距离分别相等） 实数a的绝对值是：|a|

①a为正数时，|a|=a（不变）

②a为0时， |a|=0

③a为负数时，|a|=-a（为a的相反数）

(任何数的绝对值都大于或等于0，因为距离没有负的。)

3）倒数（两个实数的乘积是1，则这两个数互为倒数） 实数a的倒数是：1/a （a0）

4）数轴（任何实数都可在数轴上表示。）

定义：如果画一条直线，规定向右的方向为直线的正方向，在其上取原点O及单位长度OE，它就成为数直线，或称数轴。

（1）数轴的三要素：原点、正方向和单位长度。

（2）数轴上的点与实数一一对应。

5）平方根（某个自乘结果等于的实数，表示为〔￣〕，其中属于非负实数的平方根称算术平方根。一个正数有两个平方根；0只有一个平方根，就是0本身；负数没有平方根。）

6）立方根（如果一个数x的立方等于a，即x的三次方等于a(x^3=a)，即3个x连续相乘等于a,那么这个数x就叫做a的立方根（cube root），也叫做三次方根）

一次函数

资料下载请点击！！

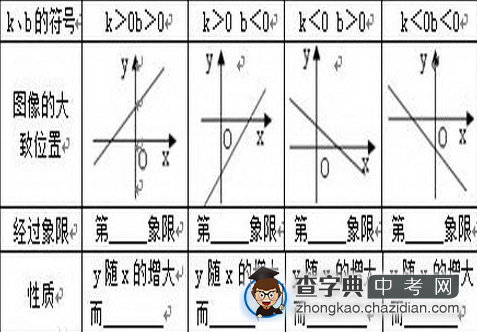
在某一个变化过程中，设有两个变量x和y，如果可以写成y=kx+b(k为一次项系数k0，b为常数)，那么我们就说y是x的一次函数，其中x是自变量，y是因变量。

一般地，形如y=kx+b(k0，k,b是常数)，那么y叫做x的一次函数。当b=0时，y=kx+b即y=kx，即正比例函数（自变量和因变量成正比例）。所以说正比例函数是一种特殊的一次函数。

还有，若自变量最高次数为1，则这个函数就是一次函数。

在某一个变化过程中，设有两个变量x和y，如果可以写成y=f（x），（即x经过某种运算得到y），即每一个x都有唯一一个y与之对应，那么我们就说y是x的函数，其中x是自变量，y随X的变化而变化。当x取一个值时，y有且只有一个值与x对应。如果有2个及以上个值与x对应时，就不是函数。

整式的乘除与因式分解

资料下载请点击！！

单项式的除法

单项式相除，把它们的系数相除，同底数幂的幂相减，作为商的一个因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式。

多项式除以单项式

多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加。

单项式除以多项式，用多项式先除以单项式的每一项，再将所得的商相加，合并同类项后取倒数。注意：是整个多项式取倒数，而不是每一项分别取倒数后合并。

因式分解定义：把一个多项式化为几个最简整式的乘积的形式，这种变形叫做把这个多项式因式分解（也叫作分解因式）。

分解因式与整式乘法为相反变形。

同时也是解一元二次方程中因式分解法的重要步骤。

因式分解没有普遍适用的方法，初中数学教材中主要介绍了提公因式法、运用公式法、分组分解法。而在竞赛上，又有拆项和添减项法，十字相乘法，待定系数法，双十字相乘法，对称多项式，轮换对称多项式法，余式定理法，求根公式法，换元法，长除法，短除法，除法等。

注意原则：

1．分解要彻底（是否有公因式，是否可用公式）

2．最后结果只有小括号

3．最后结果中多项式首项系数为正（例如：-3x2+x=x(-3x+1)）不一定首项一定为正，如-2x-3xy-4xz=-x(2+3y+4z)

衔接篇

方程特点

（1）该方程为整式方程。

（2）该方程有且只含有一个未知数。

（3）该方程中未知数的最高次数是1。

满足以上三点的方程，就是一元一次方程。

判断方法

要判断一个方程是否为一元一次方程，先看它是否为整式方程。若是，再对它进行整理。如果能整理为 ax+b=0（a0）的形式，则这个方程就为一元一次方程。里面要有等号，且分母里不含未知数。

变形公式

ax=-b（a，b为常数，x为未知数，且a0）

求根公式

通常解法

去分母去括号移项合并同类项系数化为1。

两种类型

（1）总量等于各分量之和。将未知数放在等号左边，常数放在右边。如：x+2x+3x=6。

（2）等式两边都含未知数。如：300x+400=400x，40x+20=60x[1]。