中考数学重难点第二讲——列方程解应用题的方法
发布时间:2011-01-12 17:51:04来源:查字典-中考网

从近几年的中考试题看,列方程解应用题型的试题出现在试卷上,其目的是考查学生分析问题和解决问题的能力。列方程解应用题就是将已知量与未知量的关系列成等式,通过解方程求出未知量的过程。如何解决这类题目,其方法很多,现结合实例给出几种方法,以供参考。
一、直译法
设元后,视元为已知数,根据题设条件,把数学语言直译为代数式,即可列出方程。
例1.(2004年山西省)甲、乙两个建筑队完成某项工程,若两队同时开工,12天就可以完成工程;乙队单独完成该工程比甲队单独完成该工程多用10天。问单独完成此项工程,乙队需要多少天?
解:设乙单独完成工程需x天,则甲单独完成工程需(x-10)天。根据题意,得
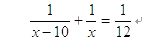
去分母,得x2-34x+120=0
解得x1=30,x2=4
经检验,x1,x2都是原方程的根,但当时x=30,x-10=20,当x=4时,x-10=-6,因时间不能为负数,所以只能取x=30。
答:乙队单独完成此项工程需要30天。
点评
:设乙单独完成工程需x天后,视x为已知,则根据题意,原原本本的把语言直译成代数式,则方程很快列出。
二、列表法
设出未知数后,视元为已知数,然后综合已知条件,把握数量关系,分别填入表格中,则等量关系不难得出,进而列出方程(组)。
例2.(2004年海淀区)在某校举办的足球比赛中规定:胜一场得3分,平一场得1分,负一场得0分。某班足球队参加了12场比赛,共得22分,已知这个队只输了2场,那么此队胜几场?平几场?
解:设此队胜x场,平y场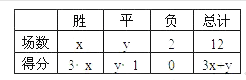
由列表与题中数量关系,得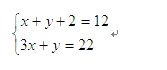
解这个方程组,得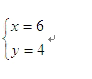
答:此队胜6场,平4场。
点评:通过列表格,将题目中的数量关系显露出来,使人明白,从胜、平、负的场数之和等于12,总得分22分是胜场、平场、负场得分之和。建立方程组,利用列表法求解使人易懂。
中考数学重难点汇总
(1)整式与分式
(2)旋转
(3)圆的基本性质
(4)投影与视图
(5)和圆有关的性质
(6)正多边形和圆的有关计算
(7)折叠剪切问题
(8)列方程解应用题的方法
(9)阅读理解题
(10)统计
Young For You—2015年武汉中考特别策划
考前
考中
考后
考前饮食
考前心理
考前冲刺
中考时间
中考作文
中考真题
中考查分
中考分数线
2011-2014年武汉各区中考分数线汇总
武昌区
江岸区
江汉区
硚口区
汉阳区
青山区

从近几年的中考试题看,列方程解应用题型的试题出现在试卷上,其目的是考查学生分析问题和解决问题的能力。列方程解应用题就是将已知量与未知量的关系列成等式,通过解方程求出未知量的过程。如何解决这类题目,其方法很多,现结合实例给出几种方法,以供参考。
一、直译法
设元后,视元为已知数,根据题设条件,把数学语言直译为代数式,即可列出方程。
例1.(2004年山西省)甲、乙两个建筑队完成某项工程,若两队同时开工,12天就可以完成工程;乙队单独完成该工程比甲队单独完成该工程多用10天。问单独完成此项工程,乙队需要多少天?
解:设乙单独完成工程需x天,则甲单独完成工程需(x-10)天。根据题意,得
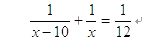
去分母,得x2-34x+120=0
解得x1=30,x2=4
经检验,x1,x2都是原方程的根,但当时x=30,x-10=20,当x=4时,x-10=-6,因时间不能为负数,所以只能取x=30。
答:乙队单独完成此项工程需要30天。
点评
:设乙单独完成工程需x天后,视x为已知,则根据题意,原原本本的把语言直译成代数式,则方程很快列出。
二、列表法
设出未知数后,视元为已知数,然后综合已知条件,把握数量关系,分别填入表格中,则等量关系不难得出,进而列出方程(组)。
例2.(2004年海淀区)在某校举办的足球比赛中规定:胜一场得3分,平一场得1分,负一场得0分。某班足球队参加了12场比赛,共得22分,已知这个队只输了2场,那么此队胜几场?平几场?
解:设此队胜x场,平y场
由列表与题中数量关系,得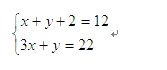
解这个方程组,得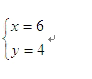
答:此队胜6场,平4场。
点评:通过列表格,将题目中的数量关系显露出来,使人明白,从胜、平、负的场数之和等于12,总得分22分是胜场、平场、负场得分之和。建立方程组,利用列表法求解使人易懂。
中考数学重难点汇总
(1)整式与分式
(2)旋转
(3)圆的基本性质
(4)投影与视图
(5)和圆有关的性质
(6)正多边形和圆的有关计算
(7)折叠剪切问题
(8)列方程解应用题的方法
(9)阅读理解题
(10)统计
Young For You—2015年武汉中考特别策划
考前
考中
考后
考前饮食
考前心理
考前冲刺
中考时间
中考作文
中考真题
中考查分
中考分数线
2011-2014年武汉各区中考分数线汇总
武昌区
江岸区
江汉区
硚口区
汉阳区
青山区