数学知识扩充：斐波那契兔子的问题

问题是指某人有一对兔子饲养在围墙中，如果它们每个月生一对兔子，且新生的兔子在第二个月后也是每个月生一对兔子，问一年后围墙中共有多少对兔子。该问题记载于公元前13世纪意大利数学家斐波那契的名著《算盘书》﹝1202﹞1228年的修订本中，并在原书中对此作了分析：第一个月是最初的一对兔子生下一对兔子，围墙内共有两对兔子。第二个月仍是最初的一对兔子生下一对兔子，共有3对兔子。到第三个月除最初的兔子新生一对兔子外，第一个月生的兔子也开始生兔子，因此共有5对兔子。继续推下去，第12个月时最终共有对377对兔子。书中还提出，每个月的兔子总数可由前两个月的兔子数相加而得。

据载首先是由19世纪法国数学家吕卡将级数{Un}：1，1，2，3，5，8，13，21，34，...{Un+1=Un+Un-1}命名为斐波那契级数，它是一种特殊的线性递归数列，在数学的许多分支中有广泛应用。1680年意大利──法国学者卡西尼发现该级数的重要关系式Un+1Un-1－Un2=(-1)n。1730年法国数学家棣莫弗给出其通项表达式：，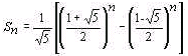

19世纪初另一位法国数学家比内首先证明这一表达式，现在称为之为比内公式。1963年美国还创刊《斐波那契季刊》来专门研究斐波那契数列。

问题是指某人有一对兔子饲养在围墙中，如果它们每个月生一对兔子，且新生的兔子在第二个月后也是每个月生一对兔子，问一年后围墙中共有多少对兔子。该问题记载于公元前13世纪意大利数学家斐波那契的名著《算盘书》﹝1202﹞1228年的修订本中，并在原书中对此作了分析：第一个月是最初的一对兔子生下一对兔子，围墙内共有两对兔子。第二个月仍是最初的一对兔子生下一对兔子，共有3对兔子。到第三个月除最初的兔子新生一对兔子外，第一个月生的兔子也开始生兔子，因此共有5对兔子。继续推下去，第12个月时最终共有对377对兔子。书中还提出，每个月的兔子总数可由前两个月的兔子数相加而得。

据载首先是由19世纪法国数学家吕卡将级数{Un}：1，1，2，3，5，8，13，21，34，...{Un+1=Un+Un-1}命名为斐波那契级数，它是一种特殊的线性递归数列，在数学的许多分支中有广泛应用。1680年意大利──法国学者卡西尼发现该级数的重要关系式Un+1Un-1－Un2=(-1)n。1730年法国数学家棣莫弗给出其通项表达式：，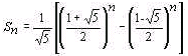

19世纪初另一位法国数学家比内首先证明这一表达式，现在称为之为比内公式。1963年美国还创刊《斐波那契季刊》来专门研究斐波那契数列。