中考数学：三角形的全等及其应用

(1)边角边公理 有两边和它们的夹角对应相等的两个三角形全等(简写成SAS)．

(2)角边角公理 有两角和它们的夹边对应相等的两个三角形全等(简写成ASA)．

推论 有两个角和其中一个角的对边对应相等的两个三角形全等(简写成AAS)．

(3)边边边公理 有三边对应相等的两个三角形全等(简写成SSS)．

(4)斜边、直角边公理 有斜边和一条直角边对应相等的两个直角三角形全等(简写成HL)．

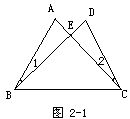
例1 如图2-1所示．1=2，ABC=DCB．求证：AB=DC．

分析 用全等三角形证明线段(或角)相等，最常用的方法是探究所求证的线段(或角)分别在一对可证的全等三角形之中．本题的AB，DC分别属于两对三角形△ABE和△CDE及△ABC和△DBC．经分析可证明△ABE≌△CDE．

证 由已知，1=2，

ABC=DCB，而

EBC=ABC-1，

ECB=DCB-2，

所以EBC=ECB．在

△ABC及△BCD中，

ABC=BCD，

EBC=ECB，BC=BC，

所以 △ABC≌△DCB(ASA)，

所以 AB=CD

说明 线段AB，CD也属于两个(事实上)全等的△ABE和△DCE，因此也可直接证明这两个三角形全等．

例2 如图2-2所示．△ABC是等腰三角形，D，E分别是腰AB及AC延长线上的一点，且BD=CE，连接DE交底BC于G．求证：GD=GE．

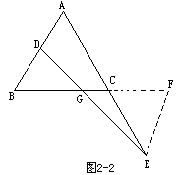
分析 从图形看，GE，GD分别属于两个显然不全等的三角形：△GEC和△GBD．此时就要利用这两个三角形中已有的等量条件，结合已知添加辅助线，构造全等三角形．方法不止一种，下面证法是其中之一．

证 过E作EF∥AB且交BC延长线于F．在△GBD及△GEF中， BGD=EGF(对顶角)， ①

B=F(两直线平行内错角相等)． ②

又B=ACB=ECF=F，所以，△ECF是等腰三角形，从而EC=EF．又因为EC=BD，所以

BD=EF． ③

△GBD≌△GEF(AAS)，

所以 GD=GE．

说明 适当添加辅助线、构造全等三角形的方法可以不止一种，本题至少还有以下两种方法：

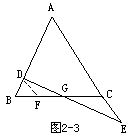
(1)过D作DF∥AC，交BC于F．可用同样方法证明△GFD≌△GCE(图2-3)．

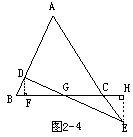
(2)过D作DFBC于F；过E作EHBC于BC延长线于H，可证明△GFD≌△GEH(图2-4)．

例3 如图2-5所示．在等边三角形ABC中，AE=CD，AD，BE交于P点，BQAD于Q．求证：BP=2PQ．

分析 首先看到BP，PQ在Rt△BPQ之中，只要证明BPQ=60(或PBQ=30)．然而，BPQ是△ABP的一个外角，所以BPQ=PAB+PBA．但A=PAB+PAC=60，若能证明PBA=PAC，问题即能解决，这两个角分别在△ABE与△CAD中，可以证明这两个三角形全等．

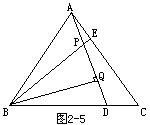
证 在△ABE与△CAD中，

EAB=DCA=60，AB=CA，AE=CD，

△ABE≌△CAD(SAS)，

所以 ABE=CAD．

由于BPQ是△ABP的外角，所以

BPQ=PAB+PBA=PAB+CAD=60．

在Rt△BQP中，BPQ=60，PBQ=30，所以BP=2PQ(在Rt△BPQ中30角的对边等于斜边的一半)．

说明 发现或构造全等三角形是利用全等三角形证明题目的关键，为此，我们常从发现两个三角形中对应元素相等入手，逐步发现或经推理凑齐三角形全等的条件．如本题在分析到欲证ABP=CAD后，进而把注意力集中到△ABE与△CAD中，这里，可适当利用几何直观感觉，启发我们寻找有希望全等的三角形，例如虽然△ABP与△APE都含欲证的角，但只需观察即可知，这两个三角形无望全等．

例4 如图2-6所示．A=90，AB=AC，M是AC边的中点，ADBM交BC于D，交BM于E．求证：

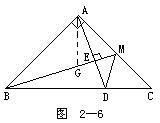
AMB=DMC．

分析1 从图形观察AME与DMC所在的两个三角形△AME与△DMC显然不全等，但是这两个三角形中有其他相等元素：AM=MC．若能利用已知条件在现有的三角形中构造出新的对应相等的元素，形成全等三角形，这是理想不过的事．由于C=45，A=90，若作A的平分线AG，则在△AGM中，GAM=45=C．结合求证中的AMB=DMC(这当然不能作为已知，但在分析中可以当作已知来考虑，以便寻找思路)，我们可以断言△AGM应该与△CDM全等！为此，只要在这两个三角形中求得一组边相等即可．图形及条件启发我们可考虑去证明△AGB≌△CDA．

证法1 作BAC的平分线AG，交BM于G．在△AGB与△CDA中，因为

AB=CA，BAG=ACD=45，

ABG=90-AMB， ①

MAD=90-EAB． ②

由于，在Rt△MAB中，AEBM，所以AMB=EAB．由①，②，ABG=MAD，所以

△AGB≌△ADC(ASA)，

于是 AG=CD．

在△AMG与△CMD中，还有

AM=MC，GAM=DCM=45，

所以 △AMG≌△CMD，

从而 AMB=DMC．

分析2 如图2-7所示．注意到在Rt△ABM中，由AEBM得到MAE=MBA，若延长AE，过C作CFAC交AE延长线于F，可构成Rt△ABM≌Rt△ACF，从而有AMB=F．设法证明DMC=F，则问题获解．

证法2 引辅助线如分析2所述．在Rt△ABM与Rt△CAF中，ABM=CAF，AB=AC，及

BAM=ACF=90，

Rt△ABM≌Rt△CAF(ASA)，

AMB=F，AM=CF． ①

在△MCD与△FCD中，FC=AM=MC(因为M是AC中点)．由于ACF=90，ACB=45，所以

FCD=MCD=45，CD=CD，

所以 △FCD≌△MCD(SAS)，

所以 F=DMC． ②

由①，② AMB=DMC．

说明 这两个证法的思路较为复杂．添加辅助线的结果造出两对全等三角形，第一对全等三角形产生一些对应相等的元素，为第二对全等三角形做了铺垫；第一对全等三角形将欲证的一个角转移到第二对全等三角形中，从而最后使问题获解．对一些较复杂的问题采用迂回的办法，因势利导地创造全等三角形，产生更多的相等条件，使欲证的角(或边)转移位置，走出死角，最终使问题获解．

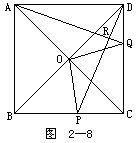
例5 如图2-8所示．正方形ABCD中，在边CD上任取一点Q，连AQ，过D作DPAQ，交AQ于R，交BC于P，正方形对角线交点为O，连OP，OQ．求证：OPOQ．

分析 欲证OPOQ，即证明COP+COQ=90．然而，COQ+QOD=90，因此只需证明COP=DOQ即可．这归结为证明△COP≌△DOQ，又归结为证明CP=DQ，最后，再归结为证明△ADQ≌△DCP的问题．

证 在正方形ABCD中，因为AQDP，所以，在Rt△ADQ与Rt△RDQ中有RDQ=QAD．所以，在Rt△ADQ与Rt△DCP中有

AD=DC，ADQ=DCP=90，

QAD=PDC，

△ADQ≌△DCP(ASA)，DQ=CP．

又在△DOQ与△COP中，

DO=CO，ODQ=OCP=45，

△DOQ≌△COP(SAS)，DOQ=COP．

POQ=COP+COQ=DOQ+COQ

=COD=90，

即OPOQ．

说明 (1)利用特殊图形的特殊性质，常可发现有用的条件，如正方形对角线互相垂直，对角线与边成45角，及OA=OB=OC=OD等均在推证全等三角形中被用到．

(2)两个三角形的全等与对应元素相等，这两者互为因果，这是利用全等三角形证明问题的基本技巧．

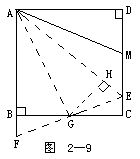
例6 如图2-9所示．已知正方形ABCD中，M为CD的中点，E为MC上一点，且BAE=2DAM．求证：AE=BC+CE．

分析 证明一条线段等于两条线段和的基本方法有两种：

(1)通过添辅助线构造一条线段使其为求证中的两条线段之和(BC+CE)，再证所构造的线段与求证中那一条线段相等．

(2)通过添辅助线先在求证中长线段(AE)上截取与线段中的某一段(如BC)相等的线段，再证明截剩的部分与线段中的另一段(CE)相等．我们用(1)法来证明．

证 延长AB到F，使BF=CE，则由正方形性质知

AF=AB+BF=BC+CE．

下面我们利用全等三角形来证明AE=AF．为此，连接EF交边BC于G．由于对顶角BGF=CGE，所以

Rt△BGF≌Rt△CGE(AAS)，

Rt△ABG≌Rt△ADM(SAS)，

过G引GHAE于H．因为AG是EAF的平分线，所以GB=GH，从而Rt△GBF≌Rt△GHE(HL)，所以

F=HEG，

则 AF=AE(底角相等的三角形是等腰三角形)，

即 AE=BC+CE．

说明 我们也可以按分析(2)的方法来证明结论，为此可先作BAE的平分线AG交边BC于G，再作GHAE于H，通过证明△ABG≌△AHG知AB=AH=BC．下面设法证明HE=CE即可，请同学们自证．

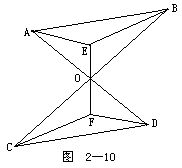
1．如图2-10所示．AD，EF，BC相交于O点，且AO=OD，BO=OC，EO=OF．求证：△AEB≌△DFC．

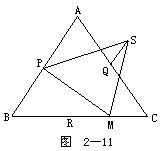
2．如图2-11所示．正三角形ABC中，P，Q，R分别为AB，AC，BC的中点，M为BC上任意一点(不同于R)，且△PMS为正三角形．求证：RM=QS．

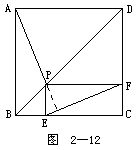
3．如图2-12所示．P为正方形ABCD对角线BD上任一点，PFDC，PEBC．求证：APEF．

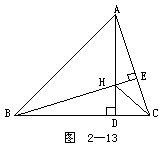
4．如图2-13所示．△ABC的高AD与BE相交于H，且BH=AC．求证：BCH=ABC．

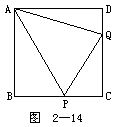
5．如图2-14所示．在正方形ABCD中，P，Q分别为BC，CD边上的点，PAQ=45．求证：PQ=PB+DQ．

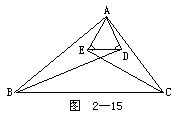
6．如图2-15所示．过△ABC的顶点A分别作两底角B和C的角平分线的垂线，ADBD于D，AECE于E．求证：ED∥BC．

练 习 十

所以

从而

于是

从而

所以

所以

所以

所以

所以

做完一道题后，再想一想还有没有其他证明方法，比较一下哪种证法更好，这对于发展思考、锻炼能力是大有好处的．

由①，②，③

利用全等三角形，我们可以得到有关角平分线、线段的垂直平分线、等腰三角形的许多重要性质，在本讲中将直接利用这些性质．

借助于全等三角形的知识，我们可以研究很多关于角和线段相等及不等问题、关于直线平行与垂直问题．

关于直角三角形有：

分析 证明一条线段等于两条线段和的基本方法有两种：

(1)通过添辅助线构造一条线段使其为求证中的两条线段之和(BC+CE)，再证所构造的线段与求证中那一条线段相等．

(2)通过添辅助线先在求证中长线段(AE)上截取与线段中的某一段(如BC)相等的线段，再证明截剩的部分与线段中的另一段(CE)相等．我们用(1)法来证明．

证 延长AB到F，使BF=CE，则由正方形性质知

AF=AB+BF=BC+CE．

下面我们利用全等三角形来证明AE=AF．为此，连接EF交边BC于G．由于对顶角BGF=CGE，所以

Rt△BGF≌Rt△CGE(AAS)，

Rt△ABG≌Rt△ADM(SAS)，

过G引GHAE于H．因为AG是EAF的平分线，所以GB=GH，从而Rt△GBF≌Rt△GHE(HL)，所以

F=HEG，

则 AF=AE(底角相等的三角形是等腰三角形)，

即 AE=BC+CE．

说明 我们也可以按分析(2)的方法来证明结论，为此可先作BAE的平分线AG交边BC于G，再作GHAE于H，通过证明△ABG≌△AHG知AB=AH=BC．下面设法证明HE=CE即可，请同学们自证．

1．如图2-10所示．AD，EF，BC相交于O点，且AO=OD，BO=OC，EO=OF．求证：△AEB≌△DFC．

2．如图2-11所示．正三角形ABC中，P，Q，R分别为AB，AC，BC的中点，M为BC上任意一点(不同于R)，且△PMS为正三角形．求证：RM=QS．

3．如图2-12所示．P为正方形ABCD对角线BD上任一点，PFDC，PEBC．求证：APEF．

4．如图2-13所示．△ABC的高AD与BE相交于H，且BH=AC．求证：BCH=ABC．

5．如图2-14所示．在正方形ABCD中，P，Q分别为BC，CD边上的点，PAQ=45．求证：PQ=PB+DQ．

6．如图2-15所示．过△ABC的顶点A分别作两底角B和C的角平分线的垂线，ADBD于D，AECE于E．求证：ED∥BC．

练 习 十

所以

从而

于是

从而

所以

所以

所以

所以

所以

做完一道题后，再想一想还有没有其他证明方法，比较一下哪种证法更好，这对于发展思考、锻炼能力是大有好处的．

由①，②，③

利用全等三角形，我们可以得到有关角平分线、线段的垂直平分线、等腰三角形的许多重要性质，在本讲中将直接利用这些性质．

借助于全等三角形的知识，我们可以研究很多关于角和线段相等及不等问题、关于直线平行与垂直问题．

关于直角三角形有：