2010年中考数学总复习：利用旋转的基本性质进行几何证明

正方形滚动一周，就是滚动四个90角。如图：滚动第一个90时，A点所经过的路线长是以点C为圆心、AC长为半径的-圆周长，此时A点滚动到了A1点(D点滚动到了D1点)；滚动第二个90时，其路线长是以点D1为圆心、A1D1长为半径的-圆周长，此时A1点滚动到了A2点的位置；滚动第三个90时，由于以点A2为圆心，此时A2点的位置未变(B2点滚动到了B3点)；滚动第四个90时其长是以点B3为圆心、B3C3长为半径的-圆周长，此时A3点滚动到了A4点的位置。A点滚动一周经过的路线长为：-8-+-8+0+-8=(4-+8)，当正方形滚动两周时，正方形顶点A所经过的路线的长等于(8-+16)。

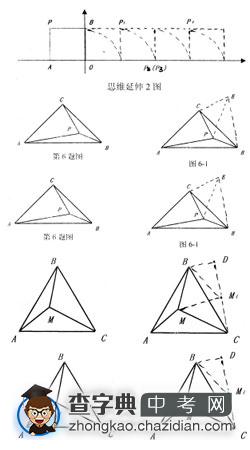
［思维延伸2］：如图2，将边长为1的正方形OAPB沿x轴正方向连续翻转2008次，点P依次落在P1、P2、P3、P4P2008的位置，则P2008的横坐标为_______。

［解析］∵正方形沿x轴正方向连续翻转4次正好翻转了一周 翻转2008次就是翻转了502周。从P点经过的路线可以看出，在每个周期内，P点相应的沿着x轴的正方向移动了4个单位长度 正方形OAPB沿x轴正方向连续翻转2008次后P点向前移动了4502=2008个单位长度 P点的横坐标为-1+2008=2007。

例6.如图6所示，已知在△ABC中，ACB=90，AC=BC，P是△ABC内一点，且PA=3，PB=1，PC=2，求BPC的度数。

［解析］可先将△APC绕点C按逆时针方向旋转90到△BEC的位置，由旋转的性质知，此时△CPE是等腰直角三角形，CPE=45，在△BPE中，由勾股定理逆定理可证出BPE=90，由此可求出BPC的度数。

［全解］将△APC绕点C按逆时针方向旋转90到△CBE的位置，连结PE △APC≌△BEC EC=PC=2，EB=PA=3，△CPE是等腰直角三角形 ∵PC=2，CPE=45PE=2-，在△BPE中 ∵(2-)2+12=32，即PE2+PB2=BE2 △BPE为Rt△，BPE=90BPC=CPE+BPE=45+90=135

［思维延伸1］如图已知，在等边三角形ABC内有一点M，且MA=3，MB=4，MC=5，求等边三角形ABC的面积。

［解析］求等边三角形的面积，关键是求出等边三角形的边长。将△AMB绕点B按逆时针方向旋转60到△CM1B的位置，连结MM1，过B点做BDCM1交CM1的延长线于点D,可得△BMM1是等边三角形 MM1=BM1=BM=4，CM1=AM=3，BM1M=60，在△MM1C中，可证M1M2+M1C2=MC2

MM1C=90，故BM1C=150BM1D=30。在Rt△BM1D中，可求出BD=2，M1D=2-。在Rt△BDC中，BC2=22+(2-+3)2=25+12- S△ABC=-BC2=-(25+12-)=9+-(单位面积)

［点评］本题的前半部分与例6类似，先求出BM1C=150，再在Rt△BM1D中，分别求出BD、M1D的长，最后在Rt△BDC中求出BC2的长，从而求出△ABC的面积。

小结：通过以上例题可以看出：

1.利用旋转的基本性质进行几何证明的关键在于如何正确的使用其基本性质。

如：例1、例2、例3、例6都运用了旋转前、后的图形全等的性质；例4运用了对应点到旋转中心的距离相等以及对应点与旋转中心所连线段的夹角等于旋转角的性质；例5则是把翻转看成了局部的旋转。

2.利用旋转的基本性质进行几何证明时，一定要找准旋转中心、旋转角和旋转方向。

正方形滚动一周，就是滚动四个90角。如图：滚动第一个90时，A点所经过的路线长是以点C为圆心、AC长为半径的-圆周长，此时A点滚动到了A1点(D点滚动到了D1点)；滚动第二个90时，其路线长是以点D1为圆心、A1D1长为半径的-圆周长，此时A1点滚动到了A2点的位置；滚动第三个90时，由于以点A2为圆心，此时A2点的位置未变(B2点滚动到了B3点)；滚动第四个90时其长是以点B3为圆心、B3C3长为半径的-圆周长，此时A3点滚动到了A4点的位置。A点滚动一周经过的路线长为：-8-+-8+0+-8=(4-+8)，当正方形滚动两周时，正方形顶点A所经过的路线的长等于(8-+16)。

［思维延伸2］：如图2，将边长为1的正方形OAPB沿x轴正方向连续翻转2008次，点P依次落在P1、P2、P3、P4P2008的位置，则P2008的横坐标为_______。

［解析］∵正方形沿x轴正方向连续翻转4次正好翻转了一周 翻转2008次就是翻转了502周。从P点经过的路线可以看出，在每个周期内，P点相应的沿着x轴的正方向移动了4个单位长度 正方形OAPB沿x轴正方向连续翻转2008次后P点向前移动了4502=2008个单位长度 P点的横坐标为-1+2008=2007。

例6.如图6所示，已知在△ABC中，ACB=90，AC=BC，P是△ABC内一点，且PA=3，PB=1，PC=2，求BPC的度数。

［解析］可先将△APC绕点C按逆时针方向旋转90到△BEC的位置，由旋转的性质知，此时△CPE是等腰直角三角形，CPE=45，在△BPE中，由勾股定理逆定理可证出BPE=90，由此可求出BPC的度数。

［全解］将△APC绕点C按逆时针方向旋转90到△CBE的位置，连结PE △APC≌△BEC EC=PC=2，EB=PA=3，△CPE是等腰直角三角形 ∵PC=2，CPE=45PE=2-，在△BPE中 ∵(2-)2+12=32，即PE2+PB2=BE2 △BPE为Rt△，BPE=90BPC=CPE+BPE=45+90=135

［思维延伸1］如图已知，在等边三角形ABC内有一点M，且MA=3，MB=4，MC=5，求等边三角形ABC的面积。

［解析］求等边三角形的面积，关键是求出等边三角形的边长。将△AMB绕点B按逆时针方向旋转60到△CM1B的位置，连结MM1，过B点做BDCM1交CM1的延长线于点D,可得△BMM1是等边三角形 MM1=BM1=BM=4，CM1=AM=3，BM1M=60，在△MM1C中，可证M1M2+M1C2=MC2

MM1C=90，故BM1C=150BM1D=30。在Rt△BM1D中，可求出BD=2，M1D=2-。在Rt△BDC中，BC2=22+(2-+3)2=25+12- S△ABC=-BC2=-(25+12-)=9+-(单位面积)

［点评］本题的前半部分与例6类似，先求出BM1C=150，再在Rt△BM1D中，分别求出BD、M1D的长，最后在Rt△BDC中求出BC2的长，从而求出△ABC的面积。

小结：通过以上例题可以看出：

1.利用旋转的基本性质进行几何证明的关键在于如何正确的使用其基本性质。

如：例1、例2、例3、例6都运用了旋转前、后的图形全等的性质；例4运用了对应点到旋转中心的距离相等以及对应点与旋转中心所连线段的夹角等于旋转角的性质；例5则是把翻转看成了局部的旋转。

2.利用旋转的基本性质进行几何证明时，一定要找准旋转中心、旋转角和旋转方向。