中考常见“实际问题与二次函数”类型题
发布时间:2009-11-17 09:51:39来源:查字典-中考网
运用二次函数的有关知识解决实际问题,是中考的热点之一,例如求销售利润的最值问题、几何图形变换中建立函数关系式的问题、以抛物线形为基础的实际问题都需要在实际的情景中去理解、分析所给的一系列数据,舍弃与解题无关的因素,建立数学模型。下面就几种常见的实际问题与二次函数类型题谈谈解题思路和方法。
一、最大利润问题
例1.某果品批发公司为指导今年的樱桃销售,对往年的市场销售情况进行了调查统计,得到如下数据:
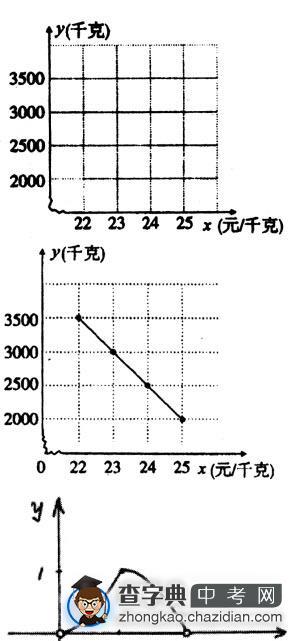
(1)在如图的直角坐标系内,做出各组有序数对(x,y)所对应的点。连接各点并观察所得的图形,判断y与x之间的函数关系,并求出y与x之间的函数关系式;
(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x(元/千克)之间的函数关系式,并求出当x取何值时,P的值最大?
分析:(1)正确描点、连线后,根据直线上两个点的坐标,可求出销售量y与销售单价x的关系式。
(2)销售利润(P)=销售量(y)单个产品的利润,将(1)结果代入后得,销售利润P为以x为自变量的二次函数,求出当x取何值时,P的值最大即求抛物线顶点横坐标。
解:(1)正确描点、连线。由图象可知,y是x的一次函数,设y=kx+b
∵点(25,2000)、(24,2500)在图象上
y=-500x+14500
(2)P=(x-13)y=(x-13)(-500x+14500)=-500x2+21000x-188500=-500(x-21)2+32000
P与x的函数关系式为P=-500x2+21000x-188500
当销售价为21元/千克时,能获得最大利润。
小结:解决此题要弄清楚题目中的数量关系,总销售额=销售量销售单价,总销售利润=销售量单个产品的利润(或总销售利润=总销售额-总成本),单件产品的利润=销售单价-产品成本。若求最大利润P值,即为求二次函数顶点纵坐标,P的最大值为32000元。
二、几何图形变换问题
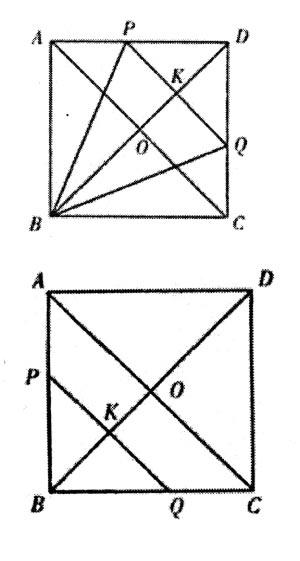
例2.已知:如图,正方形ABCD的边长为-,在对角线BD上有一动点K,过K作PQ∥AC并交正方形的两边于P、Q,设BK=x,S△BPQ=y。
求:(1)y关于x的函数关系式;
(2)画出函数图象。
分析:本题先分析出K点运动过程中,会出现两种不同情形的△BPQ,当K在BO上运动时,△BPQ为等腰直角三角形;
当K在OD上运动时,△DPQ为等腰直角三角形,而△BPQ仅为等腰三角形,故需要分两种情况讨论。
解:(1)设AC与BD相交于O
①当K在OB上时,△BPQ为等腰直角三角形
∵PBK=QBK=45
K为PQ中点
PQ=2BK=2x
y=-x2x=x2
(0
②当K在OD上运动时,△DPQ为等腰直角三角形
KD=2-x PQ=2(2-x)
y=-x2(2-x),y=-x2+2x (1x<2)
所求的函数关系式为
(2)函数图象如图所示
小结:几何变换问题在解题时,可能随着变换产生不同形状的几何图形,那么需要根据实际情况将结果用分段函数来表示,并注明相应自变量的取值范围。画图象时也应注意在自变量取值范围内,图象的变化趋势。
(周三继续刊登)
,解得:
2000=25k+b
2500=24k+b
{
k=-500
b=14500
{
y=
x2 (0
-x2+2x (1x<2)
{


运用二次函数的有关知识解决实际问题,是中考的热点之一,例如求销售利润的最值问题、几何图形变换中建立函数关系式的问题、以抛物线形为基础的实际问题都需要在实际的情景中去理解、分析所给的一系列数据,舍弃与解题无关的因素,建立数学模型。下面就几种常见的实际问题与二次函数类型题谈谈解题思路和方法。
一、最大利润问题
例1.某果品批发公司为指导今年的樱桃销售,对往年的市场销售情况进行了调查统计,得到如下数据:
(1)在如图的直角坐标系内,做出各组有序数对(x,y)所对应的点。连接各点并观察所得的图形,判断y与x之间的函数关系,并求出y与x之间的函数关系式;
(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x(元/千克)之间的函数关系式,并求出当x取何值时,P的值最大?
分析:(1)正确描点、连线后,根据直线上两个点的坐标,可求出销售量y与销售单价x的关系式。
(2)销售利润(P)=销售量(y)单个产品的利润,将(1)结果代入后得,销售利润P为以x为自变量的二次函数,求出当x取何值时,P的值最大即求抛物线顶点横坐标。
解:(1)正确描点、连线。由图象可知,y是x的一次函数,设y=kx+b
∵点(25,2000)、(24,2500)在图象上
y=-500x+14500
(2)P=(x-13)y=(x-13)(-500x+14500)=-500x2+21000x-188500=-500(x-21)2+32000
P与x的函数关系式为P=-500x2+21000x-188500
当销售价为21元/千克时,能获得最大利润。
小结:解决此题要弄清楚题目中的数量关系,总销售额=销售量销售单价,总销售利润=销售量单个产品的利润(或总销售利润=总销售额-总成本),单件产品的利润=销售单价-产品成本。若求最大利润P值,即为求二次函数顶点纵坐标,P的最大值为32000元。
二、几何图形变换问题
例2.已知:如图,正方形ABCD的边长为-,在对角线BD上有一动点K,过K作PQ∥AC并交正方形的两边于P、Q,设BK=x,S△BPQ=y。
求:(1)y关于x的函数关系式;
(2)画出函数图象。
分析:本题先分析出K点运动过程中,会出现两种不同情形的△BPQ,当K在BO上运动时,△BPQ为等腰直角三角形;
当K在OD上运动时,△DPQ为等腰直角三角形,而△BPQ仅为等腰三角形,故需要分两种情况讨论。
解:(1)设AC与BD相交于O
①当K在OB上时,△BPQ为等腰直角三角形
∵PBK=QBK=45
K为PQ中点
PQ=2BK=2x
y=-x2x=x2
(0
②当K在OD上运动时,△DPQ为等腰直角三角形
KD=2-x PQ=2(2-x)
y=-x2(2-x),y=-x2+2x (1x<2)
所求的函数关系式为
(2)函数图象如图所示
小结:几何变换问题在解题时,可能随着变换产生不同形状的几何图形,那么需要根据实际情况将结果用分段函数来表示,并注明相应自变量的取值范围。画图象时也应注意在自变量取值范围内,图象的变化趋势。
(周三继续刊登)
,解得:
2000=25k+b
2500=24k+b
{
k=-500
b=14500
{
y=
x2 (0
-x2+2x (1x<2)
{