二次函数解析式综合题求法例举
发布时间:2010-12-20 09:33:54来源:查字典-中考网
二次函数解析式的求法是二次函数知识的重点,也是中考必考内容。本文试以历年中考题为例,说明求二次函数解析式的常用方法,以期对同学们学习有所帮助。
二次函数常见的表达形式有:
(1)一般式: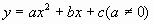 ;
;
(2)顶点式: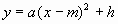 ,其中点(m,h)为该二次函数的顶点;
,其中点(m,h)为该二次函数的顶点;
(3)交点式: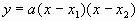 ,其中点
,其中点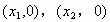 为该二次函数与x轴的交点。
为该二次函数与x轴的交点。
例1. 已知抛物线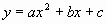 经过A,B,C三点,当
经过A,B,C三点,当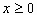 时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
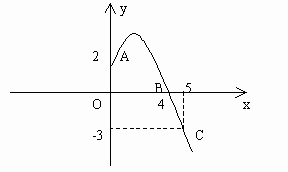
图1
分析:由图象可知,抛物线经过A(0,2),B(4,0),C(5,-3)三点,因此,可以借助二次函数一般式求出其解析式,再转化为顶点式,求出顶点坐标。
解:设所求抛物线的解析式为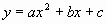 (
(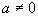 )。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
)。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
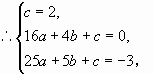 解之,得
解之,得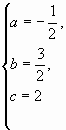
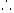 抛物线的解析式为
抛物线的解析式为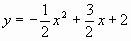
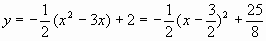
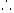 该抛物线的顶点坐标为
该抛物线的顶点坐标为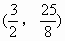 。
。
点评:这道题的一个特点是题中没有直接给出所求抛物线经过的点的坐标,需要从图象中获取信息。已知图象上三个点时,通常应用二次函数的一般式列方程求解析式。要特别注意:如果这道题是求图象所表示的函数解析式,那就必须加上自变量的取值范围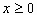 。
。
例2. 如图2,有一横截面是抛物线的水渠,水渠管理员将一根长1.5m的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,标杆有1m浸没在水中,露出水面的部分与水面成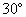 的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
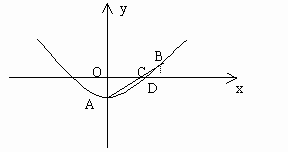
图2
分析:要求解析式,必须知道抛物线上交点的坐标。显然,由已知条件可以求出点A与点B的坐标。由于点A是所在抛物线的顶点,因此可以用抛物线的顶点式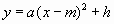 。
。
解:设AB与x轴交于点C,可知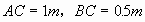 。
。
过点B作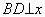 轴于点D
轴于点D
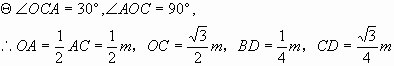
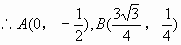
设所求水渠横截面抛物线的解析式为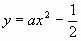 。
。
将点B的坐标代入,有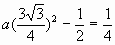 。解之,得
。解之,得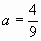 。
。
因此,该水渠横截面抛物线的解析式为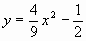 。
。
点评:解答此类问题的关键在于将实际问题的条件转化成点的坐标,再根据点的特征选择适当的函数表达式。
例3. 一条抛物线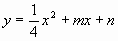 经过点
经过点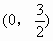 与
与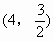 。求这条抛物线的解析式。
。求这条抛物线的解析式。
分析:解析式中的a值已经知道,只需求出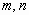 的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点
的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点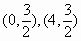 的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线
的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线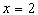 ,这样又可以从抛物线的顶点式入手。
,这样又可以从抛物线的顶点式入手。
解: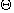 抛物线
抛物线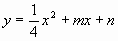 经过点(
经过点(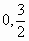 )和
)和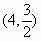 ,
,
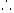 这条抛物线的对称轴是直线
这条抛物线的对称轴是直线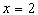 。
。
设所求抛物线的解析式为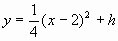 。
。
将点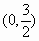 代入,得
代入,得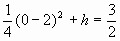 ,解得
,解得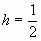 。
。
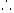 这条抛物线的解析式为
这条抛物线的解析式为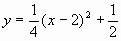 ,即
,即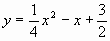 。
。
点评:当点M(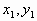 )和N(
)和N(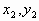 )都是抛物线上的点时,若
)都是抛物线上的点时,若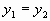 ,则对称轴方程为
,则对称轴方程为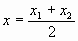 ,这一点很重要也很有用。
,这一点很重要也很有用。
例4. 如图3,在直角坐标系中,以点A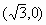 为圆心,以
为圆心,以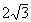 为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线
为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线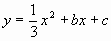 经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
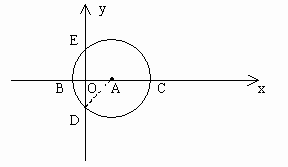
图3
分析:解题的关键在于求出点B和点C的坐标,因此需要求出线段OB,OC的长,这可根据圆的性质解决。由于点B与点C都在x轴上,因而可以根据二次函数的交点式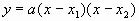 求出其解析式。
求出其解析式。
解:由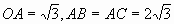 ,易得
,易得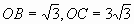
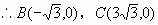
在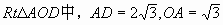 ,
,
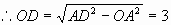 。所以点D的坐标为(0,-3)。
。所以点D的坐标为(0,-3)。
设解析式为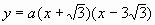 ,由条件知
,由条件知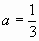 ,
,
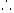 抛物线的解析式为
抛物线的解析式为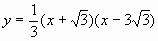
即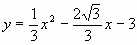
当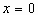 时,
时,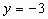 ,所以点D(0,-3)在抛物线上。
,所以点D(0,-3)在抛物线上。
点评:解这类题将点的坐标与线段的长互相转化至关重要,但要注意坐标的符号。
最后,留两道题给同学们练习。
1. 二次函数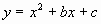 的图象经过点M(1,-2),N(-1,6)。求二次函数
的图象经过点M(1,-2),N(-1,6)。求二次函数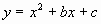 的关系式。 (答案:
的关系式。 (答案: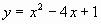 )
)
2. 已知抛物线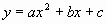 与y轴的交点为C,顶点为M,直线CM的解析式为
与y轴的交点为C,顶点为M,直线CM的解析式为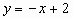 ,线段CM的长为
,线段CM的长为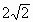 。求这条抛物线的解析式。(答案:
。求这条抛物线的解析式。(答案: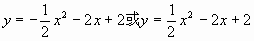 )
)
二次函数解析式的求法是二次函数知识的重点,也是中考必考内容。本文试以历年中考题为例,说明求二次函数解析式的常用方法,以期对同学们学习有所帮助。
二次函数常见的表达形式有:
(1)一般式: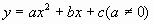 ;
;
(2)顶点式: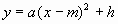 ,其中点(m,h)为该二次函数的顶点;
,其中点(m,h)为该二次函数的顶点;
(3)交点式: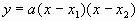 ,其中点
,其中点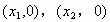 为该二次函数与x轴的交点。
为该二次函数与x轴的交点。
例1. 已知抛物线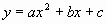 经过A,B,C三点,当
经过A,B,C三点,当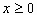 时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
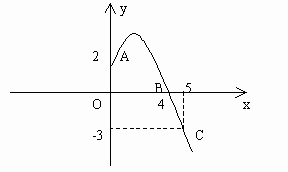
图1
分析:由图象可知,抛物线经过A(0,2),B(4,0),C(5,-3)三点,因此,可以借助二次函数一般式求出其解析式,再转化为顶点式,求出顶点坐标。
解:设所求抛物线的解析式为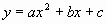 (
(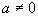 )。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
)。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
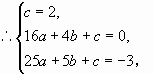 解之,得
解之,得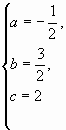
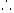 抛物线的解析式为
抛物线的解析式为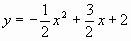
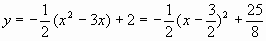
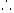 该抛物线的顶点坐标为
该抛物线的顶点坐标为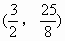 。
。
点评:这道题的一个特点是题中没有直接给出所求抛物线经过的点的坐标,需要从图象中获取信息。已知图象上三个点时,通常应用二次函数的一般式列方程求解析式。要特别注意:如果这道题是求图象所表示的函数解析式,那就必须加上自变量的取值范围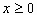 。
。
例2. 如图2,有一横截面是抛物线的水渠,水渠管理员将一根长1.5m的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,标杆有1m浸没在水中,露出水面的部分与水面成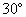 的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
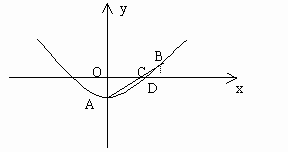
图2
分析:要求解析式,必须知道抛物线上交点的坐标。显然,由已知条件可以求出点A与点B的坐标。由于点A是所在抛物线的顶点,因此可以用抛物线的顶点式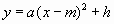 。
。
解:设AB与x轴交于点C,可知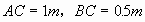 。
。
过点B作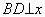 轴于点D
轴于点D
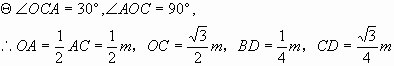
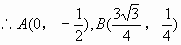
设所求水渠横截面抛物线的解析式为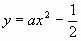 。
。
将点B的坐标代入,有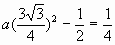 。解之,得
。解之,得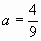 。
。
因此,该水渠横截面抛物线的解析式为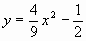 。
。
点评:解答此类问题的关键在于将实际问题的条件转化成点的坐标,再根据点的特征选择适当的函数表达式。
例3. 一条抛物线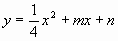 经过点
经过点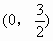 与
与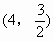 。求这条抛物线的解析式。
。求这条抛物线的解析式。
分析:解析式中的a值已经知道,只需求出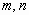 的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点
的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点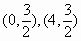 的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线
的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线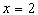 ,这样又可以从抛物线的顶点式入手。
,这样又可以从抛物线的顶点式入手。
解: 抛物线
抛物线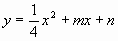 经过点(
经过点(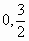 )和
)和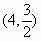 ,
,
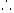 这条抛物线的对称轴是直线
这条抛物线的对称轴是直线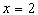 。
。
设所求抛物线的解析式为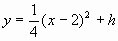 。
。
将点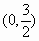 代入,得
代入,得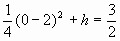 ,解得
,解得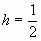 。
。
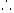 这条抛物线的解析式为
这条抛物线的解析式为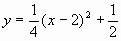 ,即
,即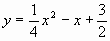 。
。
点评:当点M(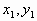 )和N(
)和N(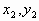 )都是抛物线上的点时,若
)都是抛物线上的点时,若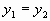 ,则对称轴方程为
,则对称轴方程为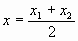 ,这一点很重要也很有用。
,这一点很重要也很有用。
例4. 如图3,在直角坐标系中,以点A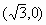 为圆心,以
为圆心,以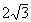 为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线
为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线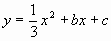 经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
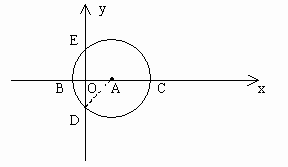
图3
分析:解题的关键在于求出点B和点C的坐标,因此需要求出线段OB,OC的长,这可根据圆的性质解决。由于点B与点C都在x轴上,因而可以根据二次函数的交点式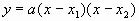 求出其解析式。
求出其解析式。
解:由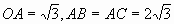 ,易得
,易得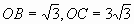
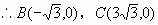
在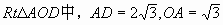 ,
,
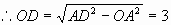 。所以点D的坐标为(0,-3)。
。所以点D的坐标为(0,-3)。
设解析式为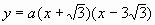 ,由条件知
,由条件知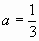 ,
,
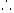 抛物线的解析式为
抛物线的解析式为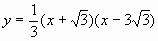
即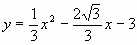
当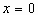 时,
时,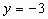 ,所以点D(0,-3)在抛物线上。
,所以点D(0,-3)在抛物线上。
点评:解这类题将点的坐标与线段的长互相转化至关重要,但要注意坐标的符号。
最后,留两道题给同学们练习。
1. 二次函数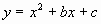 的图象经过点M(1,-2),N(-1,6)。求二次函数
的图象经过点M(1,-2),N(-1,6)。求二次函数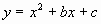 的关系式。 (答案:
的关系式。 (答案: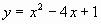 )
)
2. 已知抛物线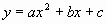 与y轴的交点为C,顶点为M,直线CM的解析式为
与y轴的交点为C,顶点为M,直线CM的解析式为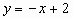 ,线段CM的长为
,线段CM的长为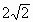 。求这条抛物线的解析式。(答案:
。求这条抛物线的解析式。(答案: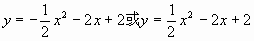 )
)