解读近几年初中数学竞赛基本走势

1、试题的价值取向。

传统竞赛强调数学形式，关注数学本身的问题，人为设置陷阱，诱使学生用特殊技巧去应对，新出现的竞赛题则更加突出数学的本质；注重数学的应用、数学的情境，关注现实生活中的数据、现象规律，应用题、情境题是这一趋势的代表：

例1 （2009年江西预赛）一个自行车轮胎，若把它安装在前轮，则自行车行驶5000km报废；若把它安装在后轮，则自行车行驶3000km后报废。行驶一定路程后可以交换前、后轮胎，如果交换前、后轮胎要使一辆自行车的一对新轮胎同时报废，那么这辆车将能行驶（）km。

2、试题所用的语言。

不只是自然语言，符号语言也重视图形语言，不仅用图形提供停息，要求考生从图形中发现规律，也可以用图形作答。图形成为数学竞赛的基本语言之一（包括几何图形、函数图象、统计图等）。

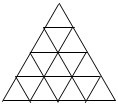
例2 （2008年全国联赛江西决赛）将正三角形每条边四等分，然后过这些分点作平行于其它两边的直线，则以图中线段为边的菱形个数为（ ）

A．15B．18C．21D．24

3、试题的类型。

题型更加丰富，不仅有常规解答题和证明题，还有发现规律的探索题、图案设计题。通过操作解决问题的实验题。

4、试题中知识的组合。不要求记忆知识，如有可能，可以用常识、经验代替知识，有许多初中赛题，如果从知识的角度分析，不过是小学水平，但必须具备初中的数学素养才能作答。

例4 （2009年江西预赛）10个人围成一个圆圈做游戏，游戏的规则是：每个人心里都想好一个数，并把自己想好的数如实地告诉他两旁的两个人，然后每个人将他两旁的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报3的人心理想的数是方块6。

例5 （2005年全国竞赛）有两副扑克牌，每副牌的排列顺序是：第一张是大王，第二张是小王，然后是黑桃、红桃、方块、梅花四种花色排列，每种花色的牌又按A，2，3，J、Q、K的顺序排列，然后从上到下把第一张丢掉，把第二张放在最底层，再把第三张丢掉，把第四张放在最底层，如此下去，直至最后只剩下一张牌，则所剩的这张牌是 。

5、试题不在单一知识上做文章，而是强调知识的联系，特别是在代数、几何、统计等多学科的交汇处挖掘素材，从而提出具有一定挑战性和综合性的问题，注重几何问题用代数方法处理，更加注重代数问题的几何意义。

1、试题的价值取向。

传统竞赛强调数学形式，关注数学本身的问题，人为设置陷阱，诱使学生用特殊技巧去应对，新出现的竞赛题则更加突出数学的本质；注重数学的应用、数学的情境，关注现实生活中的数据、现象规律，应用题、情境题是这一趋势的代表：

例1 （2009年江西预赛）一个自行车轮胎，若把它安装在前轮，则自行车行驶5000km报废；若把它安装在后轮，则自行车行驶3000km后报废。行驶一定路程后可以交换前、后轮胎，如果交换前、后轮胎要使一辆自行车的一对新轮胎同时报废，那么这辆车将能行驶（）km。

2、试题所用的语言。

不只是自然语言，符号语言也重视图形语言，不仅用图形提供停息，要求考生从图形中发现规律，也可以用图形作答。图形成为数学竞赛的基本语言之一（包括几何图形、函数图象、统计图等）。

例2 （2008年全国联赛江西决赛）将正三角形每条边四等分，然后过这些分点作平行于其它两边的直线，则以图中线段为边的菱形个数为（ ）

A．15B．18C．21D．24

3、试题的类型。

题型更加丰富，不仅有常规解答题和证明题，还有发现规律的探索题、图案设计题。通过操作解决问题的实验题。

4、试题中知识的组合。不要求记忆知识，如有可能，可以用常识、经验代替知识，有许多初中赛题，如果从知识的角度分析，不过是小学水平，但必须具备初中的数学素养才能作答。

例4 （2009年江西预赛）10个人围成一个圆圈做游戏，游戏的规则是：每个人心里都想好一个数，并把自己想好的数如实地告诉他两旁的两个人，然后每个人将他两旁的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报3的人心理想的数是方块6。

例5 （2005年全国竞赛）有两副扑克牌，每副牌的排列顺序是：第一张是大王，第二张是小王，然后是黑桃、红桃、方块、梅花四种花色排列，每种花色的牌又按A，2，3，J、Q、K的顺序排列，然后从上到下把第一张丢掉，把第二张放在最底层，再把第三张丢掉，把第四张放在最底层，如此下去，直至最后只剩下一张牌，则所剩的这张牌是 。

5、试题不在单一知识上做文章，而是强调知识的联系，特别是在代数、几何、统计等多学科的交汇处挖掘素材，从而提出具有一定挑战性和综合性的问题，注重几何问题用代数方法处理，更加注重代数问题的几何意义。